Category Theory or: How to live without elements, using arrows instead (Part II)

In the preceding post, we did a rudimentary survey of the principal elements comprising the apparatus of category theory. Henceforth, we shall direct our gaze towards the intricate constituents conjured by these foundational elements, plunging further into the intricate labyrinth of interwoven components in the machinery of category theory.

Higher Category Theory

Higher category theory deals with the generalization of parts that make up machinery. In this realm, we erect structures in a context where, between objects, we have not only mere morphisms but k-morphisms, which are maps between (k - 1) of those morphisms where \(k \in \mathbb{N}\).

Cat : Category of small categories

• This is the realm wherein categories, whose assemblage of objects coalesces into a mere set, find their dwelling. Functors serve as the conduits between these categories, linking them in \(\textbf{Cat}\).

2 Category

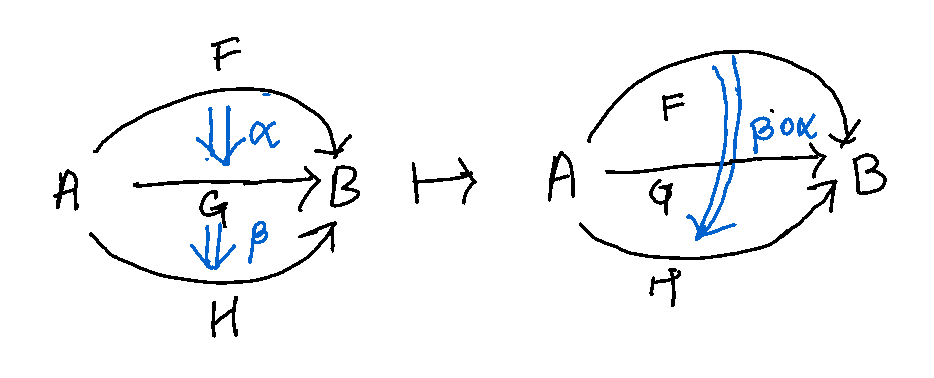
• 2-Category is the generalization of the notion of category itself. Since 2-Category is a category, it has objects and 1-morphisms; additionally, it has morphisms between 1-morphisms called 2-morphisms. Just as one can compose 1-morphisms along objects (horizontal composition), one can also compose 2-morphisms along 1-morphisms (vertical composition) as shown below.

  • Horizonal Composition, if \(F_1, G_1 : A \to B\), \(F_2, G_2 : B \to C\) and \(\alpha : F_1 \Rightarrow G_1\), \(\beta : F_2 \Rightarrow G_2\) then \(\beta \circ \alpha : (F_2 \circ F_1) \Rightarrow (G_2 \circ G_1)\),

  • Vertical Composition, if \(F, G, H : A \to B\) and \(\alpha : F \Rightarrow G\), \(\beta : G \Rightarrow H\) then,

    

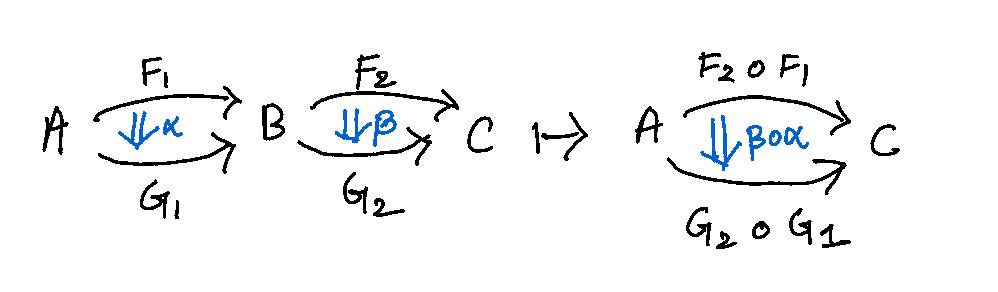
Universal Construction

Universal Property

• Meandering through a category, one is bound to find similar patterns among different constructions. A universal property abstracts these similarities and bestows significance on a generalized construction within the vast universe it inhabits. It is universal in the same sense that it describes an object in relation to the entire universe in which it lives. The universal construction encapsulates our idea of the concept that the construction conveys by determining it up-to-isomorphism; since this idea happens to come up again and again in mathematics, so do the universal constructions (maybe in a different form). In the last post, we described representable functors, limits, and co-limits; all of these are universal constructions. Here are some more constructions:

Example of Universal Property

Products

• In any category \(\mathbb{C}\) the following diagram is called the product diagram, where \(A, B, \pi_1, \pi_2, X, f, g \in\mathbb{C}\),

  

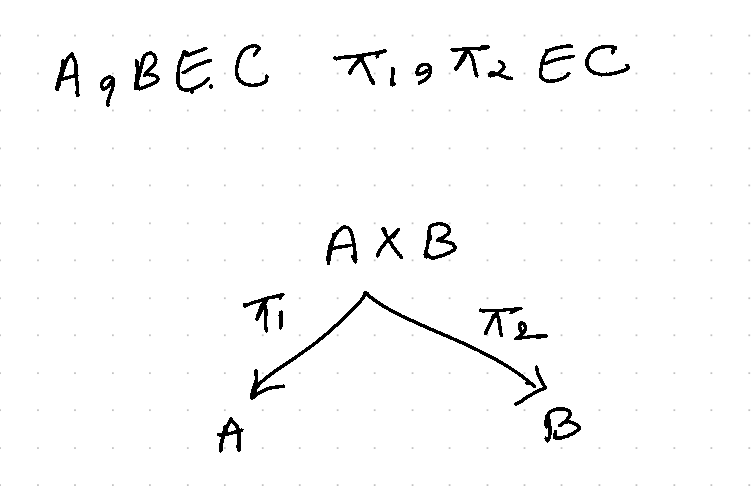
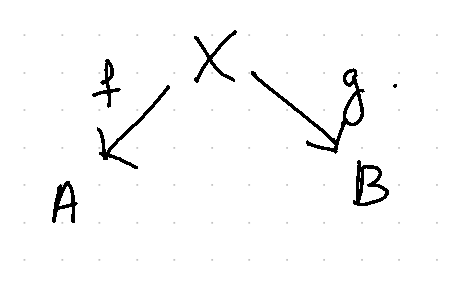
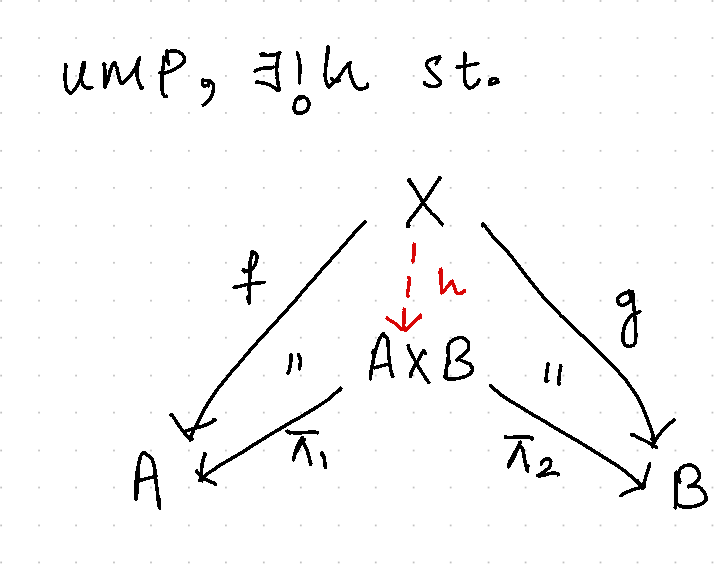
  This diagram must satisfy the following universal property: if we have a similar diagram, then there exists a unique morphism \(h: X \to A \times B\) such that,

  • \(h \circ \pi_1 = f\)
  • \(h \circ \pi_2 = g\)
  • Given any \(u : X \to A \times B\) such that \(u \circ \pi_1 = f\) & \(u \circ \pi_2 = g\) then \(u=h\).

• In almost every programming languages, you’ll find products implemented as pairs, with their distinct types and two constructors much like \(\pi_1\) and $π_2", granting access to the pair’s first and second elements, respectively.

   example :: (Int, String)
   example = (111, "Apples")
  
   number  = fst example
   string  = snd example
  

Adjunctions

Equivalence of Categories Once more…

• In the last post, we described the equivalence of categories via the functors going in and through two categories. But functors alone cannot capture this idea of equivalence completely, for they are made of two things objects and morphisms, and can at the same time be those two things. Since functors are morphisms in the category of small categories , Cat it makes sense to think about functor equivalence in terms of morphisms between functors, i.e. natural transformations. With this new knowledge, here is a better definition of the equivalence of categories. Two categories \(\mathbb{C}\) and \(\mathbb{D}\) are equal if one can find two functors \(F\) and \(G\) that go back and forth between these categories such that their composition is naturally isomorphic to the identity functor.
  • \(G \circ F \cong \mathbb{1}_{\mathbb{C}}\)
  • \(F \circ G \cong \mathbb{1}_{\mathbb{D}}\)

Adjunctions

• An adjunction is a weaker notion of equivalence defined above in the sense that it does not impose the natural isomorphism between composition of functors and identity. Instead, it imposes the existence of the following isomorphism: for \(c\in\mathbb{C}\) and \(d\in\mathbb{D}\),

  \(hom_{\mathbb{d}} (fc, d) \cong hom_{\mathbb{c}} (c, gd)\)

  

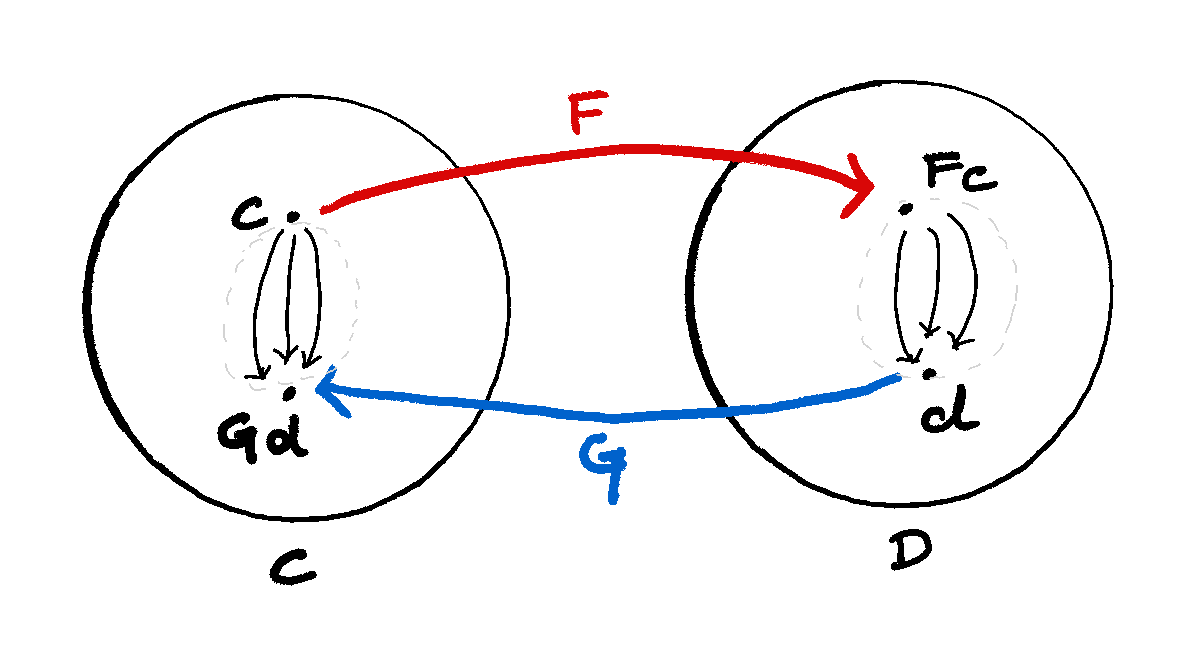
• Here, \(F\) is called the left adjoint of functor \(G\) written as \(F \dashv G\) if whenever for \(c \in \mathbb{C}\) and \(d \in \mathbb{D}\) all the maps from \(Fc \to d\) are the same as maps from \(c \to Gd\). This structure with two functors and the above isomorphism is called an adjunction.

Example of Adjunctions

Curry in Haskell

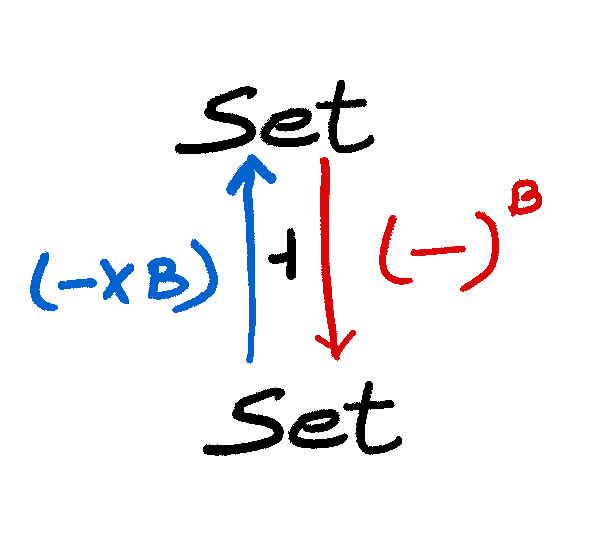
• In the category of sets (\(\textbf{Set}\)) all the objects can be combined by forming their Cartesian product. Which is just another object in \(\textbf{Set}\): \(A \times B\) which is the set of all ordered pairs \((x, y)\) such that \(x \in A\) and \(y \in B\). This construction is the same as products described earlier.

• We can also express another set or object as \(B^A\) in that it is the same as \(hom_{\textbf{Set}}(A, B)\) i.e. it has all the functions between \(A\) and \(B\).

• Now, let’s fix the set \(B\) we get from the following functors:

  \(\_ \times b : \textbf{Set} \to \textbf{Set}\) \((\_)^b : \textbf{Set} \to \textbf{Set}\)

• If one thinks of types as sets, then the morphism \(\lambda.g : \_ \to (\_)^B\) represents the function that takes in a value from some arbitrary type and returns the function type. Moreover, if we are given this \(\lambda g\) then we can easily get \(g: \_ \times B \to C\) and vice versa,

  • From, \(g: \_ \times B \to C\)

  • We can define a \(g’ : \_ \to C^B\) as \((g’(a))(b) = g (a,b)\) where \(a \in \_\) and \(b\in B\).

  • Similarly from, \(f: \_ \to C^B\)

  • We can define a \(f’: \_ \times B \to C\) as \(f’(a, b) = (f(a))(b)\) where \(a \in \_\) and \(b\in B\).

    

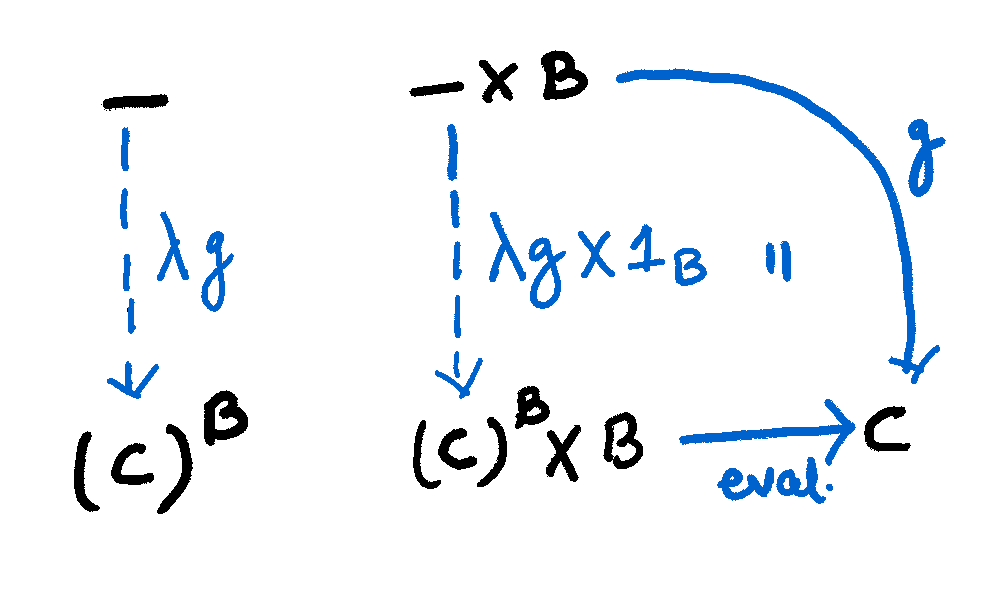
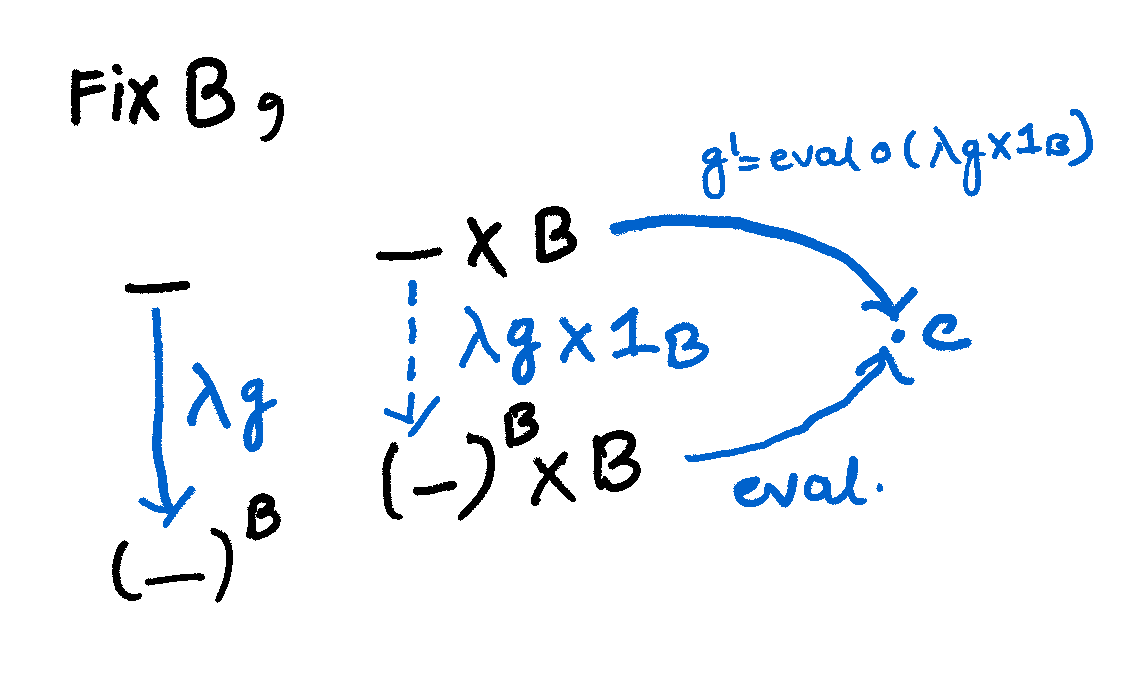
• This method of obtaining a function (with one argument) that returns another function (which takes two arguments) is called currying, and its reverse is called uncurry.

  curry :: ((a, b) -> t) -> a -> b -> t
  curry f a b = f (a, b)
  
  uncurry :: (t1 -> t2 -> t3) -> (t1, t2) -> t3
  uncurry g (a, b) = g a b
  

• Similarly, one can show that there is a canonical bijection here that programmers can understand intuitively, i.e.,

  \(hom_{\textbf{Set}} (A \times B, C) \cong hom_{\textbf{Set}} (A, C^B)\)

• Since we now have two functors and an isomorphism, we’ve got ourselves an adjunction here for every set \(B\).

  

Connections of Galois

• This example requires some jargon,

  • Partially Ordered Sets: A set where elements have order among them, i.e., some way to compare every single element but it is partial in the sense that pairs of elements need not be comparable.
  • Monotone Functions: These are the functions between ordered sets that preserve the order, i.e., when plotted, they either increase or decrease throughout their domains.

• Now, let \((A, \leq)\) and \((B, \leq)\) be two partially ordered sets, and then the (monotone) Galois connection between these posets consists of two monotone functions: \(f : A \to B\) and \(g : B \to A\), such that for all \(a \in A\) and \(b \in B\),

  \(f(a) \leq b\) if and only if \(a \leq g(b)\)

  From the lens of category theory, one can say that a Galois connection is nothing but an adjoint \(f \dashv g\) equipped with the essential property that an upper or lower adjoint of a Galois connection uniquely determines the other:

  • \(f(a)\) is the least element \(minB\) in set \(B\) when \(a \leq g(minB)\).
  • \(g(b)\) is the largest element \(maxA\) in set \(A\) when \(f(maxA) \leq b\).

Monads

Monoid

Classical monoid

• A monoid is defined as a set with an associative binary operation and a special element that acts as a unit with respect to that set.
• Example: the set of natural numbers \(\mathbb{N}\) for a monoid with addition or multiplication as the operation and \(0\) or \(1\) as the unit, respectively.

Category of Monoids

• We want to think of classical monoid in terms of morphisms. So, imagine we have a set (\(S\)) and a binary function (\(f\)) that operates on the elements of that set. Moreover, if one of the inputs to this function is a special element of \(S\) called unit then the output of the function is the same as the second input, whatever that may be.
• We thus define monoid as a single object category. Since it’s a single object, we have a single hom-set which is the set that has all the morphisms from the object to itself.
• The interesting thing is that we can get the same results from going inside the object and using the function (multiply or add etc.) and composing the function in the before-mentioned hom-set.

Monad

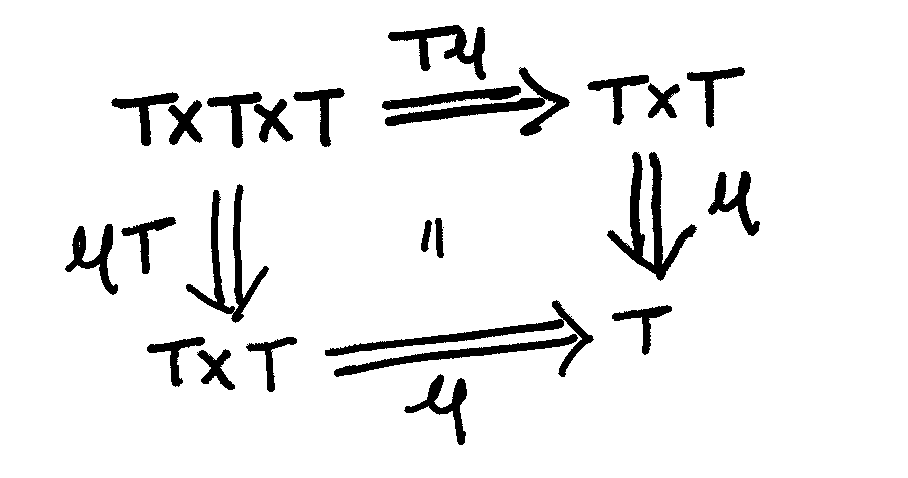
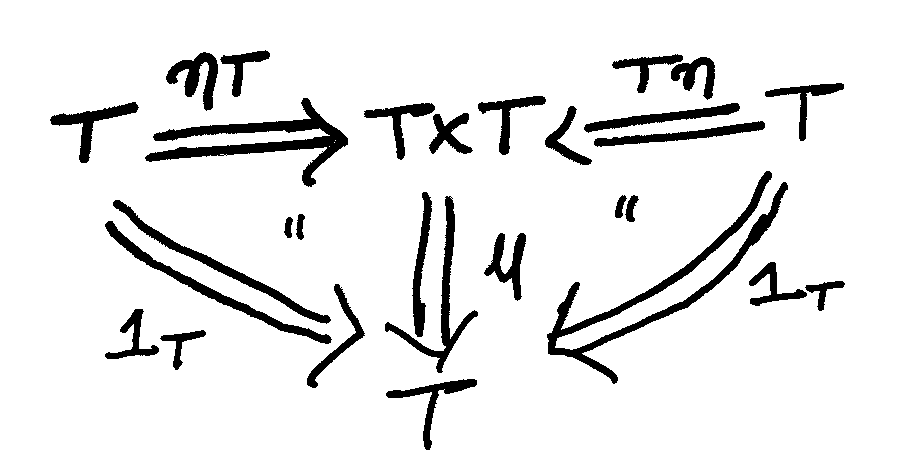
• A monad on some category \(\mathbb{C}\) is a triple \((T,\eta,\mu)\) which consists of,

  • A functor, \(T : \mathbb{C} \to \mathbb{C}\).
  • A unit natural transformation, \(\eta : \mathbb{1}_{\mathbb{C}} \Rightarrow T\).
  • A multiplication natural transformation, \(\mu : T \times T \Rightarrow T\).

  such that the following diagrams in the functor category \(\mathbb{C}^{\mathbb{C}}\) commute, i.e. to say for all \(c \in \mathbb{C}\) the following diagrams commute when functors are applied to \(c\) (\(Tc\)) and when components of natural transformations (\(\eta_c\), \(\mu_c\)) are considered, then these diagrams commute in \(\mathbb{C}\),

  Associativity Square:

  Unit Triangles:

• One may also say that a monad is a generalization of monoid.

Examples of Monads

A Monad for moniod in the \(\textbf{Set}\)

• \(\mathbb{C} = \textbf{Set}\)
• \(T : X \to X^\star\) where \(X\) is a classical monoid in \(\textbf{Set}\) and \(X^\star\) is the kleene star over \(X\).
• \(\eta_x : Tx \to x^\star\) for all \(x \in X\)
• \(\mu_x : x^{\star\star} \to x\) for all \(x \in X\)
• For unit triangles, consider, \(x = (a, b, c)\) where \(x \in X\) then,
  • \(T (\eta (x)) = ((a), (b), ( c))\)
  • \(\mu (T (\eta (x))) = x\)
  • Similarly,
  • \(\mu (\eta (T x)) = x\)
• Similarly, associativity square.

Monads in Computer Science

• In this world, programs denote the morphisms between objects \(A\) and \(TB\) where \(A\) is the object of values of type \(A\) and \(TB\) is the object of computations of type \(B\). These programs are functions that are generated through a maze of computations.

• For the existence of a monad in such a category, these programs must form a kliesli category.

• A kliesli triple over \(\mathbb{C}\) is the triple \((T, \eta, \_^\star)\) where,

  • \(T: Obj(\mathbb{C}) \to Obj(\mathbb{C})\)
  • To give values to a computation: \(\eta_A : A \to TA\) where \(A \in \mathbb{C}\).
  • An extension to \(f\) from values to computation to computation to computation: \(f^\star : TA \to TB\) for \(f: TA \to TB\)
  • \(\eta_A^\star = \mathbb{1}_{TA}\)
  • \(\eta_A;f^\star = f\)
  • \(f^\star ; g^\star = (f;g)^\star\)

  The equations for kliesli triples form a category, i.e. the kliesli category (\(\mathbb{C}_T\)) such that given a kliesli triple \((T, \eta, \_^\star)\) , \(\mathbb{C}_T\) is defined as,

  • \(Obj(\mathbb{C}_T) = Obj(\mathbb{C})\)
  • \(hom_{\mathbb{C}_T} (A,B)\) of the programs between \(A\) to \(B\) is the same as the hom set \(hom_{\mathbb{C}} (A, TB)\).
  • The identity of \(A \in \mathbb{C}_T\) is \(\eta_A : A \to TA\).
  • \(\forall f \in hom_{\mathbb{C}_T}(A,B), g \in hom_{\mathbb{C}_T}(B,C)\) we have that \(f \circ g^\star: A \to TC\).

Monads in Haskell

• In Haskell,
  • \(T\) corresponds to a parameterized type.
  • \(\eta\) corresponds to return in Prelude.
    • `return: a → Ta`
  • \(\_^\star\) corresponds to >>=.
    • ~>>=: (a → Tb) -> (Ta → Tb)~

class Monad where
  return :: a -> m a
  (>>=)  :: m a -> (a -> m b) -> m b

• Monad of partiality, \(TA = A + {\bot}\) where \(\bot\) denotes divergent computation is expressed in Haskell as the algebraic data type `Maybe`,

  instance Monad Maybe where
    return a = Just a
    m >>= f = case m of
                Just x  -> f x
                Nothing -> Nothing
  
  divide :: Maybe Int -> Maybe Int -> Maybe Int
  divide a b = a >>= \m -> b >>= \n -> if n == 0 then Nothing else return (a `div` b)
  

• Monad for side effects: A side effect is a form of computation where the computation changes state. It can be changing stuff inside variables or raising an exception. We can express such a notion by \(TA = (A \times S)^S\) where \(S\) is a set of states.

  • \(\eta_A\) maps \(a \mapsto (\lambda (s:S). \llbracket a, s \rrbracket)\)
  • if \(f : A \to TB\) and \(c \in TA\) then \(f^\star( c)= \lambda (s:S).(\text{let} \ \llbracket a, s’ \rrbracket = c(s) \ \text{in} \ f(a)(s’))\)

  instance Monad (State s) where
    return a = State (\s -> (s, a))
    State m >>= f = State (\s -> let (s', a) = m s
                                   State m' = f a
                                  in m' s')
  
  readState :: State s s
  readState = State (\s -> (s, s))
  
  writeState :: s -> State (s, ())
  writeState s = State (\s -> (s, ()))
  
  -- Example
  increment :: State Int ()
  increment = readState >>= \s -> writeState (s + 1)
  

References

The above material comes from my notes made while reading, watching,

• Tom Leinster, Basic Category Theory
• Eugenia Cheng, TheCatsters: Monads
• Bartosz Milewski, Category Theory for Programmers
• Emily Riehl, Category Theory in Context
• Eugenio Moggi, Computational Lambda Calculus and Monads
• Eugenio Moggi, Nick Benton and John Hughes Monads and Effects