Category Theory or: How to live without elements, using arrows instead (Part I)
Jun. 4, 2023After my recent attempt to learn the core of category theory and exploration of Saunders Mac Lane’s insightful books, I have tried to organize my notes, thoughts, and highlights in this post. The post is divided into two parts: the origins of category theory are covered in the first one, and next comes the core machinery for working with categories.
Origins
Mathematics is said to have its origins in “human cultural activities,” as Mac Lane put it. These activities lead to some ideas, like the activity of observing, which leads to a notion of the “symmetry” of objects, and this general idea of “symmetry” is then formalized as a symmetry group of figures or formulae (which when defined on an infinite set becomes a transformation group). This perspective comes from the intuitionists, who argue that mathematics is a human construct, not an objective truth, and that is to say that there would be no math without the brain. The ideas that have their origins in these activities are said to have some intuitive content, which can then be formalized. By formal, we mean a list of rules, axioms, or methods of proof that can be applied without attention to the “meaning” but which give results that do have the correct interpretation.
| Activity | Idea | Formalization |
|---|---|---|
| Argue | Proof | Logical Connectives |
| Choosing | Chance | Probability |
| Counting | Next | Successor; Ordinal Number |
| Observing | Symmetry | Transformation Group |
If we consider mathematics to be the science of number and space, then we can construct some formal notions. It is the morphosis of fact into form.
What is the idea of the formal?
- To describe the idea of the formal, a few basic mathematical structures are required. To put this in context, here’s a quote from Mac Lane,
- These mother structures include sets, transformations, groups, order, and topology. These are the building blocks of more complex structures that evolve within mathematics.
Where does category theory come from?
- Category theory originates from the distaste for set theory among mathematicians. Set theory is convenient and enough to describe almost all mathematical objects. Therefore, as a foundation for mathematics, set theory is widely accepted with a condition that we must live with formally undecidable theorems. Moreover, the word “set” is not really defined because of the circular nature, and we also need to have ZF axioms to get around paradoxes. ZF axioms do not settle the continuum hypothesis, i.e., they hold for some models but don’t for others.
- There are relations (like membership) on sets, which can also be nicely done using the composition of functions. This leads to an alternate foundation for mathematics using categories.
Category Theory as a Foundation for Mathematics
We can use set theory as a foundation, primarily because essentially all mathematics is reducible to sets. Another way to look at this is that instead of looking at mathematics as a whole, it’s better viewed as its objects and mappings between them. This approach works for numerous branches of mathematics.
| Branch | Objects | Morphisms/Mappings |
|---|---|---|
| Set Theory | Sets | Functions |
| Topology | Topological Spaces | Continuous Maps |
| Groups | Groups | Homomorphism |
| Euclidean Geometry | Inner Product Spaces | Orthogonal Transformations |
Machinery of Category Theory
What is a Category?
A category \(\mathbf{C}\) consists of
- a collection of objects: \(A\), \(B\), \(C\),
- a collection of arrows: \(f\), \(g\), \(h\),
- for each arrow \(f\) objects \(\mathrm{dom}_{f}\) and \(\mathrm{cod}_{f}\) called the domain and codomain of \(f\). If \(\mathrm{dom}_{f}=A\) and \(\mathrm{cod}_{f}=B\), we also write \(f :A\to B\),
- given \(f :A\to B\) and \(g :B\to C\) , so that \(\mathrm{dom}_{g}=\mathrm{cod}_{f}\), there is an arrow \(g\circ f:A\to C\),
- an arrow \(\mathbf{1}_{A}:A\to A\) for every object \(A\) of \(\mathbf{C}\),
- such that the following laws are valid,
- Associative law: for every \(f:A\to B\), \(g :B\to C\) and \(h :C\to C\) we have \(h\circ(g\circ f)=(h\circ g)\circ f\).
- Unit law: for every \(f:A\to B\) we have \(f\circ\mathbf{1}_{A} = f = \mathbf{1}_{B}\circ f\) where \(\mathbf{1}_{A}\) is the identity morphism.
Since, anything that satisfies this definition is a category, we can say that category theory is abstract algebra of arrows.
To construct a category, this question has to be answered, given a mathematical structure, what are the morphisms preserving this structure? which, in turn, gives us the arrows of a category.
In each category \(\mathbf{C}\) with two objects \(a\) and \(b\) there exists a collection,
\(hom(a,b) \ = \ \{f \ | \ f \ \text{is an arrow of} \ \mathbf{C} \ \text{and} \ f:a \to b\}\)
\(\textbf{hom-set}\) is not always a set, as occasionally, it might be too big to be considered under the ZF axioms.
Examples, of categories,
- Set is a category of sets and set theoretic functions as morphisms. This is a category of mathematical object without any structure, and since we associate arrows to enforce structure, the morphisms in Set are special relations which themselves are basically sets of input-output pairs.
- Opposite Category, is a category which exists as a dual of any other category. It is constructed by reversing the direction of all the arrows in, let’s say \(\mathbf{C}\) and keeping the objects the same to get \(\mathbf{C}^{op}\). Since, \(\mathbf{C}^{op}\) is the dual of \(\mathbf{C}^{}\) the product in \(\mathbf{C}\) becomes the sum in \(\mathbf{C}^{op}\), the terminal object becomes the initial and so on.
- Product Category, is a category which is constructed from two categories \(\mathbf{C}\) and \(\mathbf{D}\) such that the objects in the product category (\(\mathbf{C} \times \mathbf{D}\)) are pairs \(\llbracket c,d \rrbracket\) and all the morphisms are pairs of arrows i.e for every \(f : a \to b\) in \(\mathbf{C}\) and \(g : a’ \to b’\) in \(\mathbf{D}\) we have \(\langle f,g \rangle\) in \(\mathbf{C} \times \mathbf{D}\).
Functors
- When we ask, “What are morphisms that preserve this structure?” with mathematical structure under consideration, categories themselves, then the structure preserving morphisms, are called functors or covariant functors. There are arrows between categories. This means that categories (small ones) form a category (\(\mathbf{Cat}\)) with functors as arrows.
- A category itself is a sort of formalization of the intuitive idea of “structure” and, as we’ve seen, it has two components, viz., objects and morphisms. Similarly, to preserve
this structure a functor between two categories \(\mathbf{C}\) and \(\mathbf{D}\) must also have two component functions,
- \(\mathit{F}_0 : x \ \rightarrow \ F(x)\) where \(x \in \mathbf{C}\) and \(F(x) \in \mathbf{D}\).
- \(\mathit{F}_1 : f \ \rightarrow \ F(f)\) where \(f\) is an arrow in \(\mathbf{C}\) as \(f: x \to y\) and \(F(f)\) is an arrow in \(\mathbf{D}\) as \(F(f):
F(x) \to F(y)\).
- such that for each \(x , y \ \in \ Obj(\mathbf{C})\), \(F_{x,y} \ : \ \mathbf{C}(x,y) \to (\mathbf{D}(F(x), F(y)))\) between \(\textbf{hom-set}s\) such that,
- it preserves the source and targets of morphisms.
- it preserves identity morphisms i.e \(F(\mathbf{1}_{x}) = \mathbf{1}_x\) where \(x \in Obj(\mathbf{C})\).
- it preserves compositions of morphisms i.e the image of composition of morphisms under \(F\) is composition of their images i.e \(F(g \circ f) = F(g) \circ F(f)\).
- such that for each \(x , y \ \in \ Obj(\mathbf{C})\), \(F_{x,y} \ : \ \mathbf{C}(x,y) \to (\mathbf{D}(F(x), F(y)))\) between \(\textbf{hom-set}s\) such that,
- These functors embed the source category into the target category as they may only cover a part of the target category yet all objects in the source category must have a function to produce an object in target, but the not all objects in the target are supposed to be pointed by these functors.
Functor Composition
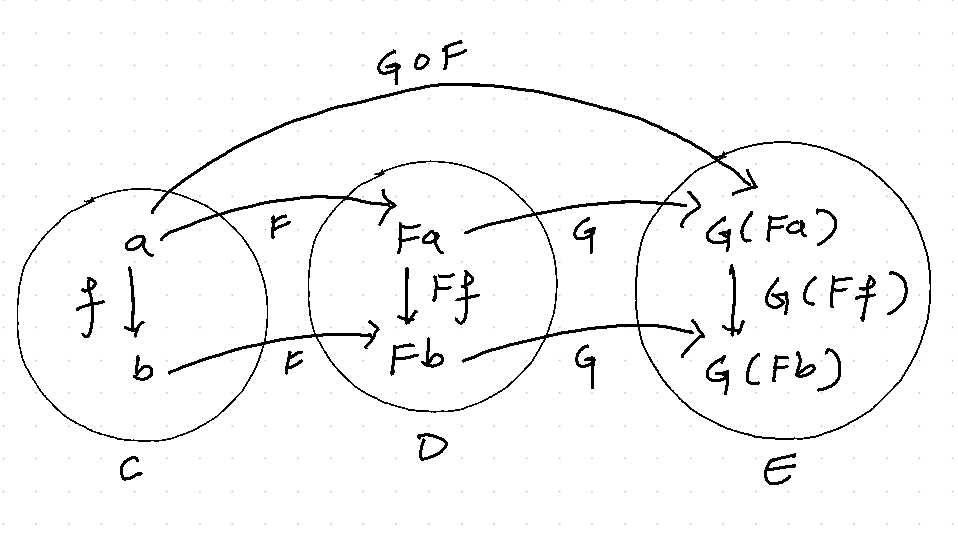
Important Functors
- Constant Functor \(\Delta_c\) is the functor that maps all the objects from the source category into a single object (\(c\)) in the target category and all the morphisms into a single morphism that is the \(\mathbf{1}_c\).
- BiFunctors are the functors that map pairs of objects and pairs of arrows from \(\mathbf{C} \times \mathbf{C}\) to objects and arrows in \(\mathbf{C}\).
- Contravariant Functors are the functors from \(\mathbf{C}^{op}\) to \(\mathbf{C}\) that basically lift the opposite arrows.
- Profunctors are the functors that go from the product of a category and its opposite to the category of sets, i.e. from \(\mathbf{C} \times \mathbf{C}^{op}\) to Set.
- Representable Functors
We know that morphisms between any two objects (\(a,b\)) in a category (\(\mathbf{C}\)) form a set called \(\textbf{hom}_{\mathbf{C}}(a,b)\). This set also happens to be an object in the category Set. We can, thus, have a functor (covariant representable functor) that goes from any category (\(\mathbf{C}\)) to the category of sets (\(\textbf{Set}\)), moreover, if we fix the source object and vary the target object i.e
\(\forall a \in \mathbf{C} \ , \ \textbf{hom}_\mathbf{C}(a,\_) \ : \ \mathbf{C} \to \textbf{Set}\)
where,
- \(\textbf{hom}_\mathbf{C}(a,b) = \{f \in \mathbf{C} \ | \ f:a\to b\}\) where \(b \in \mathbf{C}\).
- action of this functor on an arrow \(g: b \to c\),
- \(\textbf{hom}_\mathbf{C}(a,g) : \textbf{hom}_\mathbf{C}(a,b) \to \textbf{hom}_\mathbf{C}(a,c)\) defines as,
- \(\textbf{hom}_{\mathbf{C}}(a,g) = g \circ f\).
- \(\textbf{hom}_\mathbf{C}(a,g) : \textbf{hom}_\mathbf{C}(a,b) \to \textbf{hom}_\mathbf{C}(a,c)\) defines as,
As we are fixing the source \(a\) the functor \(\textbf{hom}_{\mathbf{C}}(a, \_)\) combines all arrows from \(a\) to somewhere in \(\mathbf{C}\). On the other hand, if we were to fix the target \(b\) the functor \(\textbf{hom_{\mathbf{C}}(\_, b)\) should combine all arrows coming to \(b\) since functors preserve the source and destination of objects,
\(\forall b \in \mathbf{C} \ , \ \textbf{hom}_{\mathbf{C}}(\_,b) \ : \ \mathbf{C}^{op} \to \textbf{Set}\)
this is a contra-variant representable functor and is defined as,
- \(\textbf{hom}_{\mathbf{C}}(\_,b) = \_ \circ g’\) where \(b \in \mathbf{C}\).
- action of this functor on some arrow \(g’ : a’ \to a\),
- \(\textbf{hom}_{\mathbf{C}}(g’,b) \ : \ \textbf{hom}_{\mathbf{C}}(a,b) \to \textbf{hom}_{\mathbf{C}}(a’,b)\) defined as,
- \(\textbf{hom}_{\mathbf{C}}(g’,b) = \_ \circ g’\).
- \(\textbf{hom}_{\mathbf{C}}(g’,b) \ : \ \textbf{hom}_{\mathbf{C}}(a,b) \to \textbf{hom}_{\mathbf{C}}(a’,b)\) defined as,
From above, we can say that \(\textbf{hom}_{\mathbf{C}}\) is a hom-functor,
\(\textbf{hom}_{\mathbf{C}}(\_,\_) \ : \ \mathbf{C}^{op} \times \mathbf{C} \to \textbf{Set}\)
which maps,
- a pair of objects \(a.b \in \mathbf{C}\) to set \(\textbf{hom}_{\mathbf{C}} (a,b)\) in Set category.
- a pair of morphisms \(f,g \in \textbf{hom}_{\mathbf{C}}\), \(f: a’ \to a\) and \(g : b \to b’\) to single morphisms (function) in Set, \(\textbf{hom}_{\mathbf{C}}(f,g) : \textbf{hom}_{\mathbf{C}} (a,b) \to \textbf{hom}_{\mathbf{C}}(a’,b’)\) defined as \(\textbf{hom}_{\mathbf{C}}(f,g) : h \mapsto g \circ h\circ f\).
Natural Transformations
When we ask “what are morphisms that preserve this structure?” with mathematical structure under considerations as functors then the structure preserving morphisms are called natural transformations.
Given two categories \(\mathbf{C}\) and \(\mathbf{D}\) and functors \(F : \mathbf{C} \to \mathbf{D}\), \(G : \mathbf{C} \to \mathbf{D}\) we define a natural transformation as, \(\alpha : F \Rightarrow G\) such that,
- \(\alpha\) assigns every object a in \(\mathbf{C}\), the arrow \(\alpha_a : Fa \to Ga\) in \(\mathbf{D}\) such that,
- any \(f : a \to b\) in \(\mathbf{C}\) we have, \(\alpha_b \circ F(f) = G(f) \circ \alpha_a\).
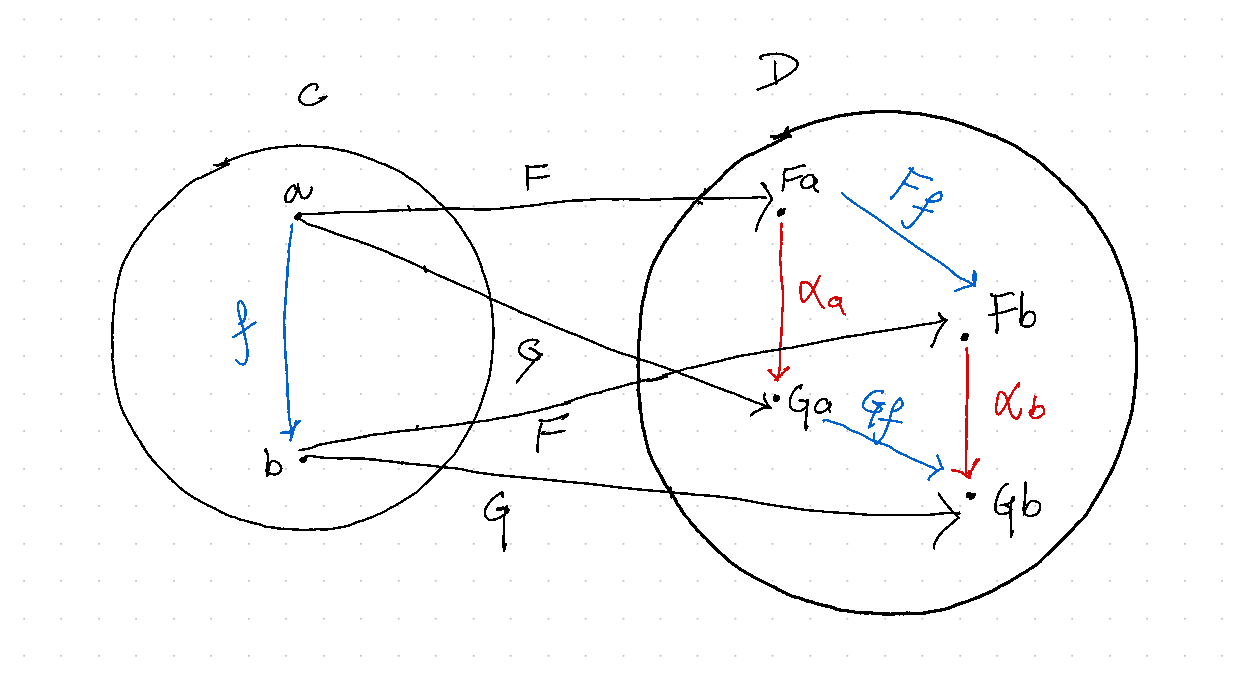
- \(\alpha\) assigns every object a in \(\mathbf{C}\), the arrow \(\alpha_a : Fa \to Ga\) in \(\mathbf{D}\) such that,
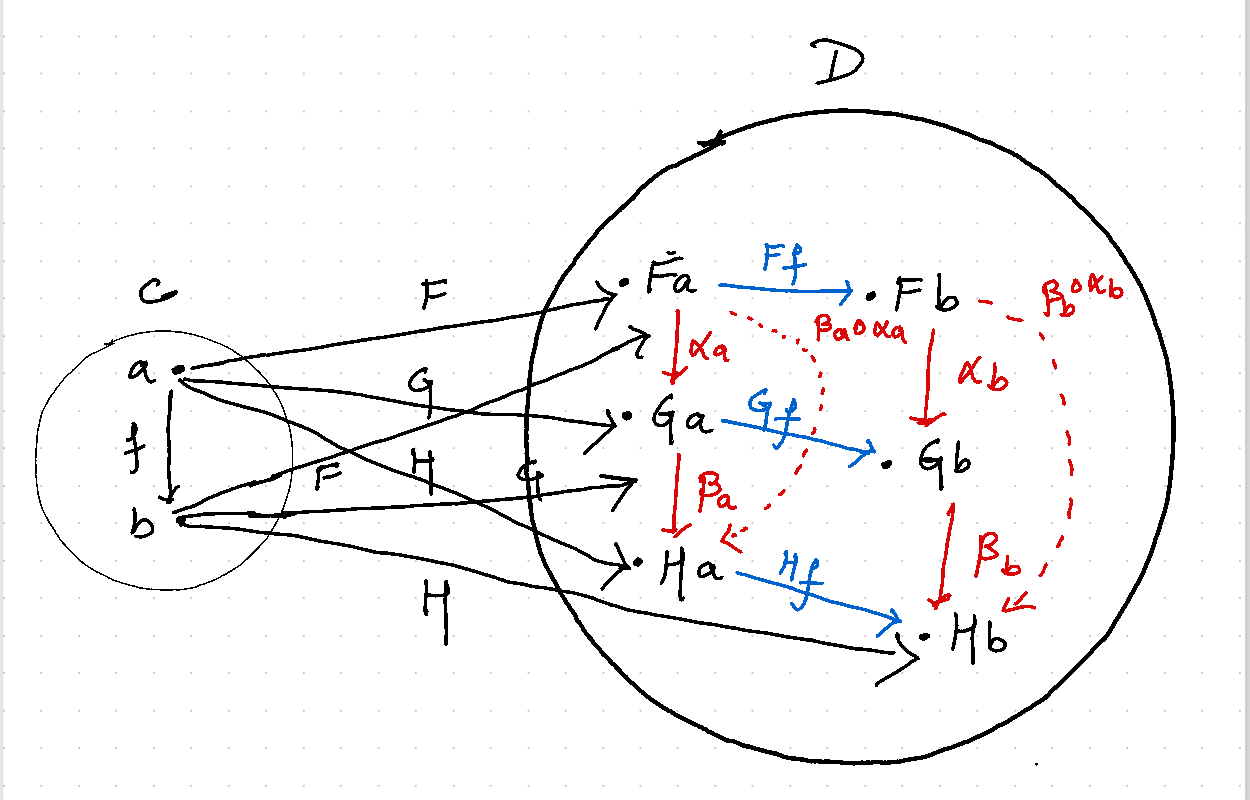
Composition of Natural Transformations
Consider two fuctors \(F,G\) between two categories \(\mathbf{C}, \mathbf{D}\) such that a natural transformation,
\(\alpha : F \to G\)
is taken to be any rule that takes an object \(a \in \mathbf{C}\) and an arrow \(\alpha_a : Fa \to Ga\) in a way that the following diagram commutes for every arrow \(f : a\to b\) where \(f \in\mathbf{C}\) , In other words, \(Gf \circ \alpha_a = \alpha_b \circ Ff\) for all \(f\).
We can compose natural transformations as depicted visually by the following diagram where we have three functors \(F,G,H\) between \(\mathbf{C}\) and \(\mathbf{D}\),
Functor Category
- We can now try to make a category of functors as now we can compose two natural transformations to get an arrow between two functors.
- Therefore, given two categories \(\mathbf{C}\) and \(\mathbf{D}\) the functor category \(\mathbf{D}^{\mathbf{C}}\) such that,
- \(\textbf{objects}(\mathbf{D}^{\mathbf{C}}) = \{F \ | \ \text{F is a functor,} \ F : \mathbf{C} \to \mathbf{D} \}\)
- \(\textbf{arrows}(\mathbf{D}^{\mathbf{C}}) = \{\alpha \ | \ \alpha \ \text{is a ntf.} \ \alpha : F \to G \}\)
- Are the previous two structures sets?
- No, they’re too big to be sets. But we have something better, we can construct a functor category, \(\textbf{Set}^{\mathbf{C}}\) which is the category of all set-valued functors or “diagrams” from \(\mathbf{C}\) to \(\textbf{Set}\). This category is not illegitimately big rather it is as big as \(\textbf{Set}\) and extremely useful as we can embed any category \(\mathbf{C}\) into \(\textbf{Set}^{\mathbf{C}}\) which comes equipped with advanced category theoretic tools which may not present in \(\mathbf{C}\). This is possible by using \(\textbf{hom-set}\) functor that maps \(\mathbf{C}\) into \(\textbf{Set}^{\mathbf{C}}\).
Natural Isomorphisms
A natural isomorphism is an isomorphism in a functor category. If \(F : \mathbf{C} \to \mathbf{D}\) and \(G : \mathbf{C} \to \mathbf{D}\) are two functors, a natural isomorphism between them is a natural transformation \(\eta : F \Rightarrow G\) whose components are isomorphisms. In this case, the inverse natural transformation \(\eta^{−1} : G \Rightarrow F\) is given by \((\eta^{-1})_A = (\eta_A)^{-1}\). We write \(F \cong G\) when F and G are naturally isomorphic.
Equivalence of Categories
An equivalence (\(\simeq\)) of categories is a pair of functors, \(F\) and \(G\) such that,
- \(G \circ F = \mathbf{1}_{\mathbf{C}}\)
- \(F \circ G = \mathbf{1}_{\mathbf{D}}\)
Limits
According to nLab ,
“In category theory a limit of a diagram \(D:\mathbf{J}\to \mathbf{C}\) in a category \(\mathbf{C}\) is an object \(Lim_D\) of \(\mathbf{C}\) equipped with morphisms to the objects \(Dj\) for all \(j\in \mathbf{J}\), such that everything in sight commutes. Moreover, the limit \(lim_D\) is the universal object with this property, i.e. the “most optimized solution” to the problem of finding such an object.”
Let’s try to unpack this definition and generalize this notion of \(lim_D\). Consider two categories \(\mathbf{C}\) and \(\mathbf{J}\) with two functors \(D\) and \(\Delta_x\). The objects in \(\mathbf{J}\) are indexed \(1,2,3\cdots\) thus, objects in \(\mathbf{C}\) become \(D1,D2,D3\cdots\) and \(D\) takes some objects from \(\mathbf{J}\) with their morphisms to \(\mathbf{C}\). And another collapsing constant functor \(\Delta_x\) that collapses all objects into a single object \(x\) in \(\mathbf{C}\) and all morphisms into the single identity morphism \(\mathbf{1}_x\).
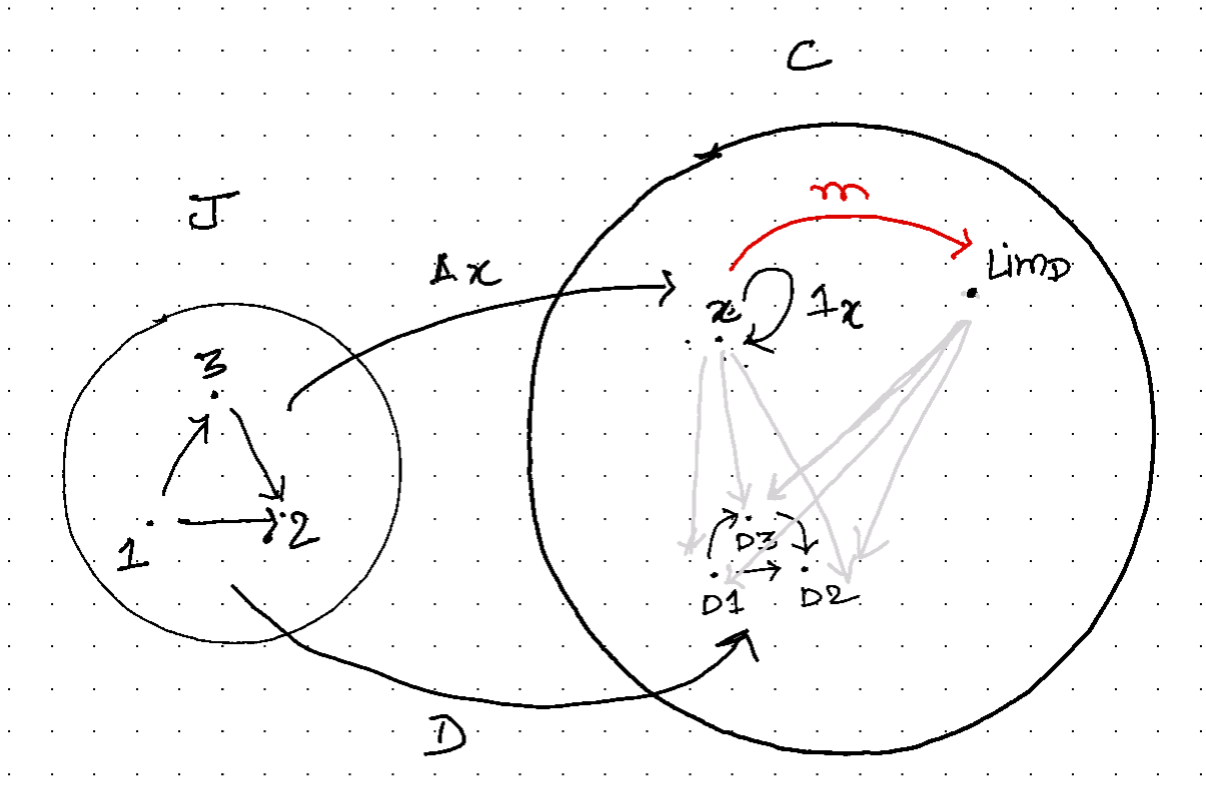
Two constructions emerge,
Cone :
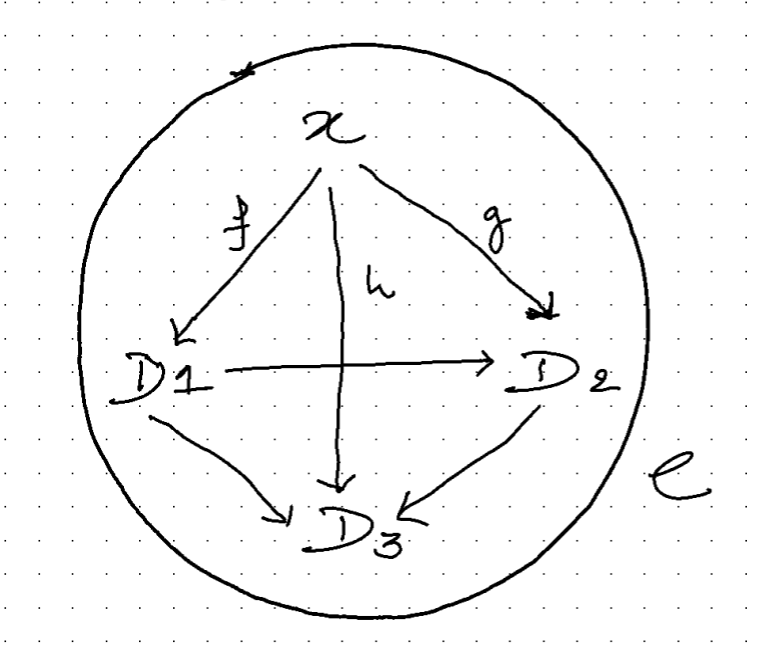
Co-Cone :
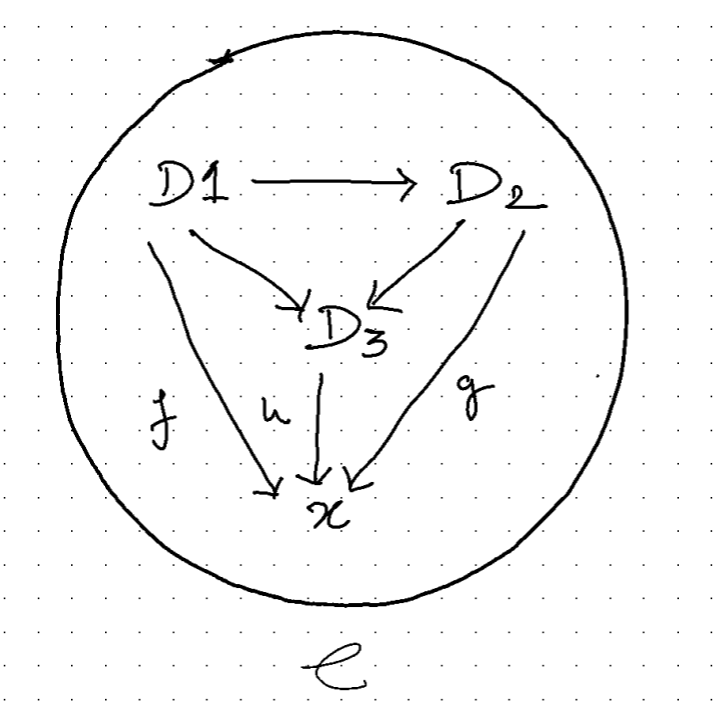
Now, let’s try to construct a category of cones where we want to have the before-mentioned cones as objects and the unique morphism between \(LimD\) and \(x\) (which can be any other apex of some cone). So let \(m\) to be that morphism between cones such that all the triangles of the following form commute.
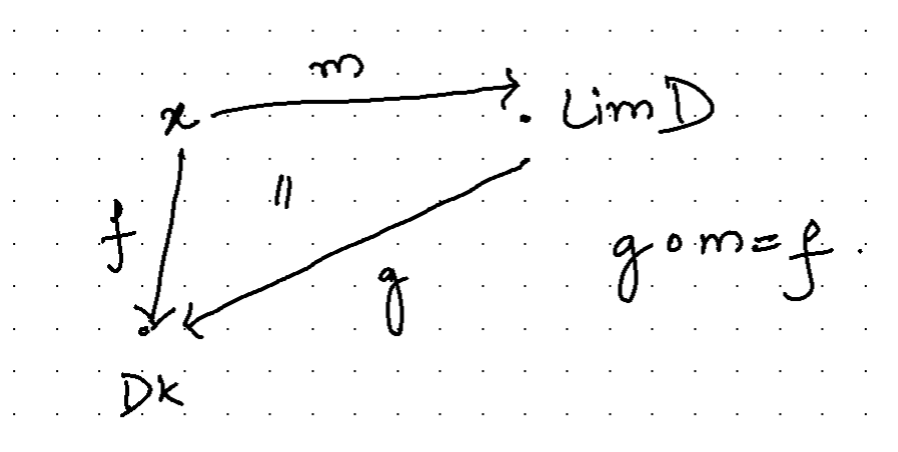
The terminal object of this category is called the limit.
Furthermore, we have natural transformations between the two functors \(D\) and \(\Delta_x\). Since there can be any number of such natural transformations, they form a \(\textbf{hom-set}_{\mathbf{C}^{\mathbf{J}}} (D,\Delta_x)\) in the functor category \(\mathbf{C}^{\mathbf{J}}\) where \(D\) and \(\Delta_x\) are just objects. Moreover, this hom-set is also a member of the category \(\textbf{Set}\).
For a natural transformation \(\alpha : \Delta_x \to D\). We have two hom-sets,
- One hom-set of natural transformations between the two functors, \(\textbf{hom-set}_{\mathbf{C}^{\mathbf{J}}} (\Delta_x, D)\).
- One hom-set of the morphisms between apices and limit, \(\textbf{hom-set}_{\mathbf{C}} (x, LimD)\).
Similarly, we have two functors that go from \(\mathbf{C} \to \textbf{Set}\),
- One functor goes from \(x \to \textbf{hom}_{\mathbf{C}^{\mathbf{J}}} (\Delta_x, D)\).
- One functor goes from \(x \to \textbf{hom}_{\mathbf{C}}(x, LimD)\).
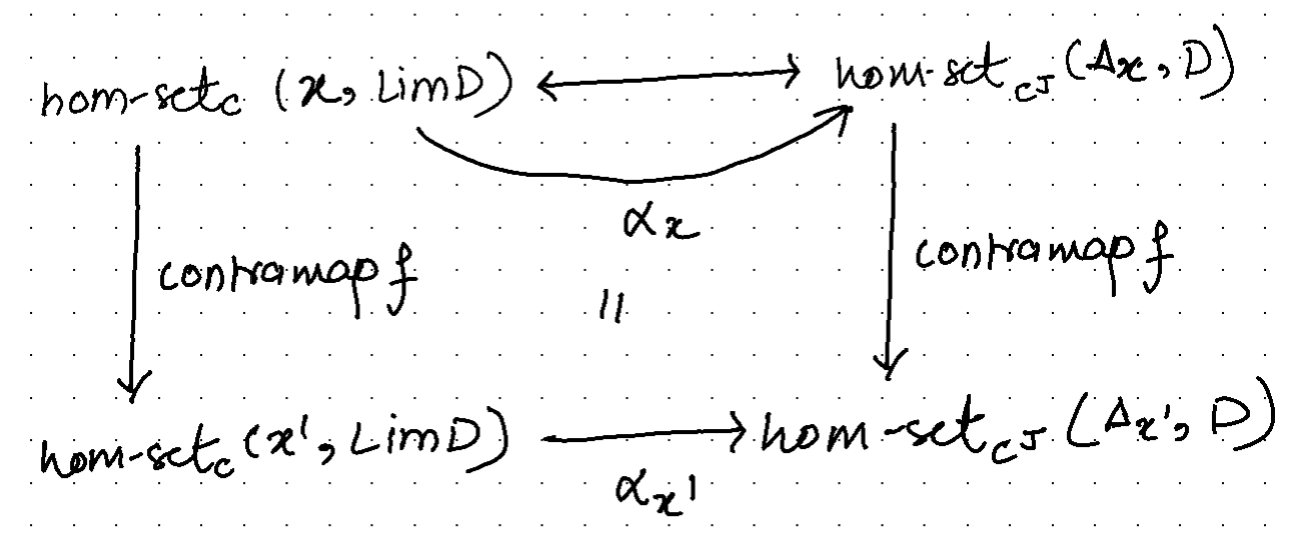
We want to show that the morphism (α) between the above hom-sets is a natural transformation.
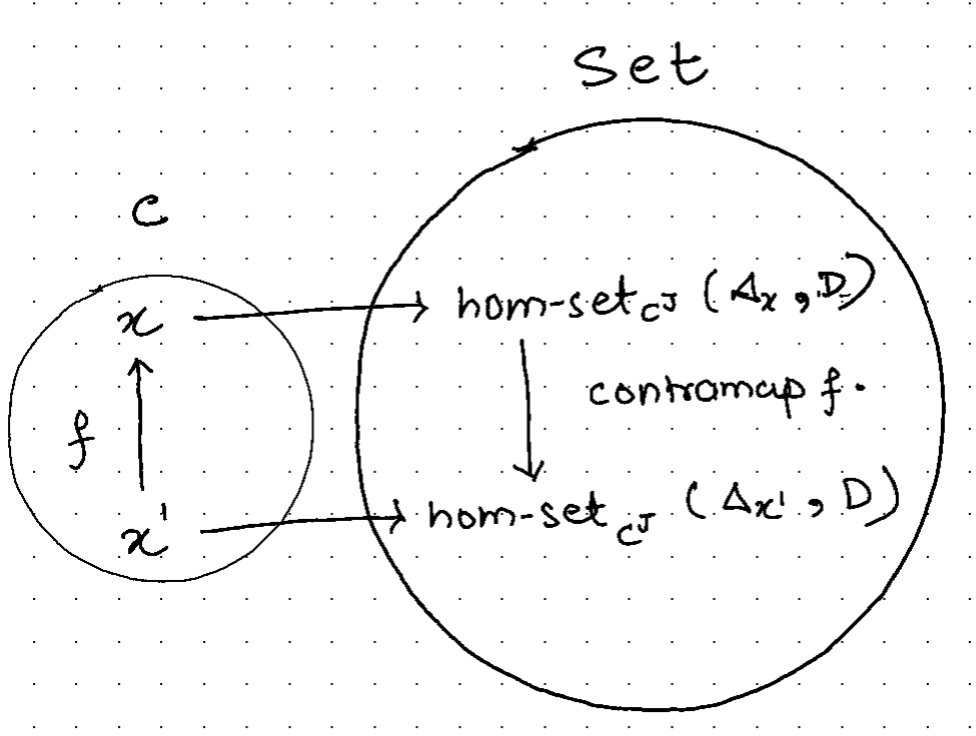
To show that consider natural transformations \(\mu\) and \(\gamma\) such that,
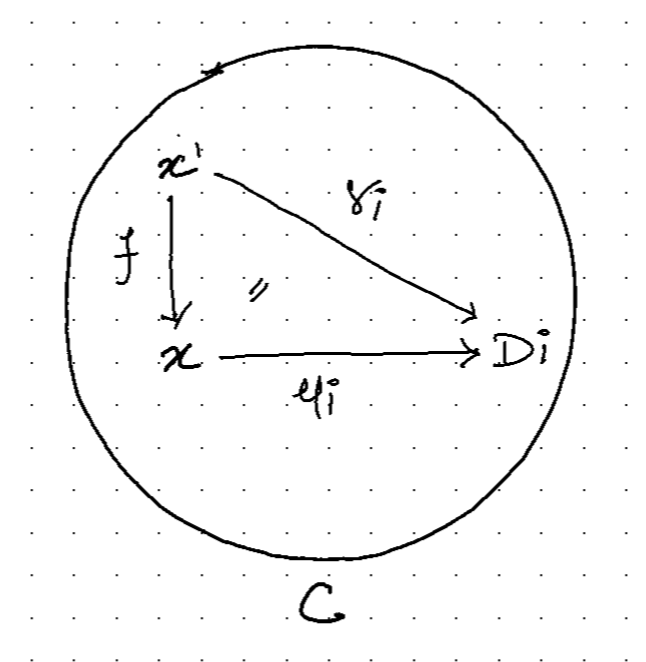
- \(\mu \in \textbf{hom-set}_{\mathbf{C}^{\mathbf{J}}} (\Delta_x, D)\), \(\mu_i \ : \ x \to Di\).
- \(\gamma \in \textbf{hom-set}_{\mathbf{C}^{\mathbf{J}}} (\Delta_{x’}, D)\), \(\gamma_i \ : \ x’ \to Di\).
- It is apparent from below diagram that such triangles commute i.e \(\gamma_i = \mu_i \circ f\).
Similarly in Set,
- \(u \in \textbf{hom-set}_{\mathbf{C}}^{} (x, LimD)\), \(u_i \ : \ x \to Di\)
- \(v \in \textbf{hom-set}_{\mathbf{C}}^{} (x’, LimD)\), \(v_i \ : \ x’ \to Di\), \(v_i = u_i \circ f\)
Therefore for \(\alpha\) to be a natural transformation, the naturality condition must hold, and all such squares must commute.
Category of Presheaves
Presheaf
A presheaf is a functor, \(F: \mathbf{C}^{op} \to \textbf{Set}\) such that for any \(x \in \mathbf{C}\), \(Fx\) in \(\textbf{Set}\) is the set that represents the ways \(x\) can occur in \(F\) and any mapping \(f: x \to y\) where \(f,y \in \mathbf{C}\) the corresponding \(Ff : Fy \to Fx\) maps each of the \(y\)’s of \(Fy\) to each of the \(x\)’s in \(Fx\).
Representable Presheaf
The above presheaf \(F\) becomes a representable when it is naturally isomorphic to a hom-functor \(\textbf{hom}_{\mathbf{C}} (\_ , X) : \mathbf{C}^{op} \to \textbf{Set}\) which maps any object \(c \in \mathbf{C}\) to the hom-set \(\textbf{hom}_{\mathbf{C}} (c , X)\) and each \(f : c’ \to c\) where \(f, c’ \in \mathbf{C}\) to the function which maps each morphism \(c \to X\) to the composite \((c’ \to c) \to X\). Here the object \(X\) is determined uniquely upto an isomorphism in \(\mathbf{C}\) and is called the representing object.
Yoneda Lemma
“The set of morphisms from a representable presheaf \(y( c)\) into an arbitrary presheaf \(X\) is in natural bijection with the set \(X( c)\) assigned by \(X\) to the representing object \(c\).”
In simple words if we have a functor \(F\) that goes from \(\mathbf{C} \to \textbf{Set}\) then the natural transformation between \(F\) and the hom-functor \(\textbf{hom}_{\mathbf{C}} (\_ , c)\) corresponds by a natural isomorphism (set theoretic bijection) to the set \(Fc\).
Proof Sketch
Consider the category of presheaves on a locally small category \(\mathbf{C}\), viz. \(\textbf{Set}^{\mathbf{C}^{op}}\) with an incoming functor \(y\) from \(\mathbf{C}\),
\(y : C \to \textbf{Set}^{\mathbf{C}^{op}} \\ \forall c \in \mathbf{C}, \ y = c \mapsto \textbf{hom}_{\mathbf{C}}(\_ , c)\)
\(y\) sends each object of \(\mathbf{C}\) to the hom-functor into that object i.e presheaf represented by \(c\).
We want to prove that for any \(X \in \textbf{Set}^{\mathbf{C}^{op}}\) there is an isomorphism between the hom-set of the presheaf functors from \(y( c)\) to \(X\) and the value of \(X\) at \(c\).
\(\textbf{hom}_{\textbf{Set}^{\mathbf{C}^{op}}}(y( c),X) \cong X( c)\)
Consider the following diagram,
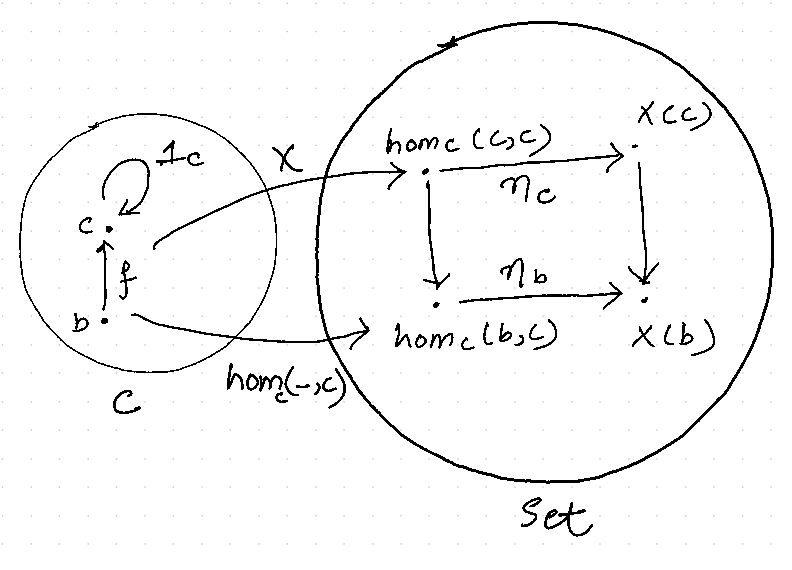
Since we know that,
- \(\mathbf{1}_c \in \textbf{hom}_{\mathbf{C}} (c,c)\)
- \(\eta_c (\mathbf{1}_c) \in X( c)\)
- \(f \in \textbf{hom}_{\mathbf{C}} (b,c)\)
- \(\eta_b (f) \in X(b)\)
We can have a similar diagram with elements instead of sets,
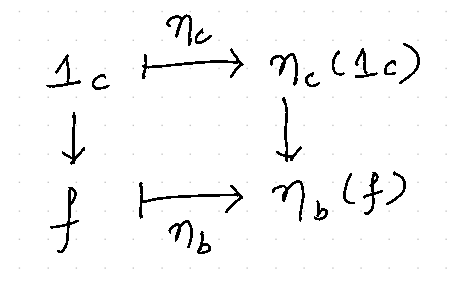
From above it is clear that the set of natural transformations of form, \(\eta : \textbf{hom}_{\mathbf{C}} (\_, c) \Rightarrow X\) is completely determined by a value \(\eta_c (\mathbf{1}_c) \in X( c)\). This means that to show the naturality condition on any \(\eta : \textbf{hom}_{\mathbf{C}} (\_, c) \Rightarrow X\) it is sufficient to show that \(\eta\) is already fixed by some value \(\eta_c(\mathbf{1}_{\mathbf{C}}) \in X( c)\) of its component \(\eta_c : \textbf{hom}_{\mathbf{C}} (c,c) \to X( c)\) on \(\mathbf{1}_{\mathbf{C}}\).
In other words, each object of \(\mathbf{C}\) is uniquely specified by the arrows into it (or out of it), up to isomorphism. The objects of a category can be uniquely defined in terms of the role they play in the category and in terms of their interactions with the whole.